제어 이론 기본 개념

제어 관련 기초적인 내용을 정리하여 공유한다.

제어 배경 지식

Laplace 변환

Time domain 함수 $f(t)$ 를 s-domain 함수 $F(s)$ 로의 변환을 말한다.

개념은 어려울 수 있는데 이해하기 보단

미분방정식을 풀기 위한 도구라고만 알아두자.

라플라스 변환을 통해 복잡한 미분방정식을

간단한 대수방정식으로 바꾸어 풀 수 있다.

그리고 시간 영역에서 풀기 어려운 문제를

다른 영역에서 해석하면 유용한 정보를 추출할 수 있다.

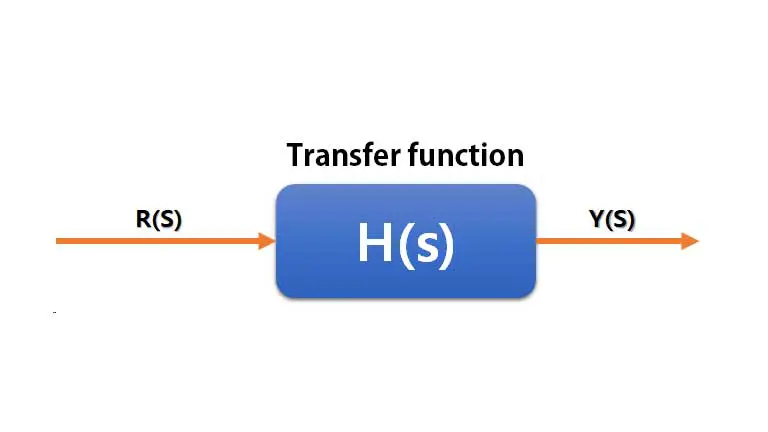
Transfer function

이런 장점을 ‘전달 함수‘ 에서 잘 볼 수 있다.

$H(s)=\frac{Output(s)}{Input(s)}=\frac{(s-b_1)\cdots(s-b_m)}{(s-a_1)\cdots(s-a_n)}$

위와 같이 정의되고 함수 $H(s)$ 가 Input을

어떻게 변화시킬 지 직관적으로 보여준다.

예를 들어 Input(s)의 해 $a_1,\cdots,a_n$ 중

어느 하나라도 실수 값이 양수라면 Ouput은 발산한다.

이 말을 간단하게 정리하면 다음과 같다.

$\forall Re(a_i)<0$ 일 때 $H(s)$ 는 stable하다.

TF는 미적분과정까지 포함해 하나의 분수 형태로 표현할 수 있다.

보통 Input 과 Output 에 따라 다음 표와 같이 Plant, Controller 를 구분한다.

명칭	Input	Output
Controller	기준값	제어입력
Plant	제어입력	측정값, State

Feedback 제어

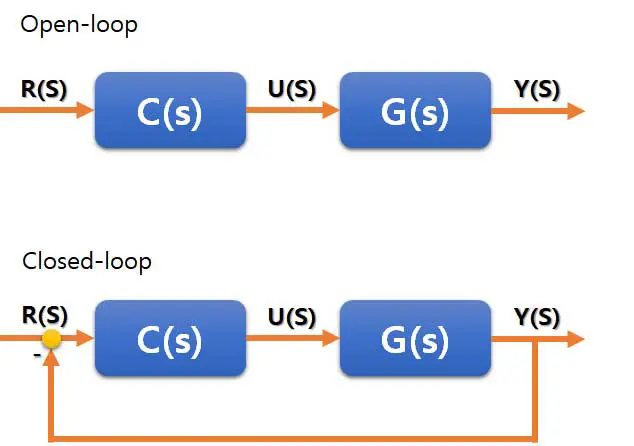
Open-loop controller

위에 나오듯 기준값으로만 제어 입력을 계산하는 것을

Open-loop 제어기라고 부른다.

이 때 Open-loop TF는 다음과 같이 구할 수 있다.

$Y=CGR$

$\rightarrow H_{OL}(s)=\frac {Y(s)}{R(s)}=CG$

따라서 Y가 R을 정확히 추종하기 위해서는 $C=G^-1$ 가 되어야한다.

G에 오차가 있는 경우 그만큼 오차 E가 발생한다.

Closed-loop controller

아래 diagram처럼 기준값과 측정값의 차이를 이용하는 것을

Closed-loop 제어기라고 한다.

이 때 Closed-loop TF는 다음과 같다.

$Y=CG(R-Y)$

$\rightarrow (1+CG)Y=CGR$

$\rightarrow H_{CL}(s)=\frac {Y(s)}{R(s)}=\frac{CG}{1+CG}$

G에 대한 정보가 없더라도 $C \rightarrow \infty$ 라면 $H_{CL} \rightarrow I$ 이기때문에

손쉽게 오차를 최소화 할 수 있다.

위의 예시처럼 측정값을 제어에 사용하는 걸 Feedback 제어라고 한다.

$H_{OL},H_{CL}$ 를 각각 Open-loop,Closed-loop 게인이라고도 말하며

기호로는 $L(s)$ 로 나타낸다.

외란, 잡음이 존재할 때의 제어

좀 더 General한 경우 저주파 외란 $W(s)$ 와 고주파 잡음 $V(s)$ 가 존재한다.

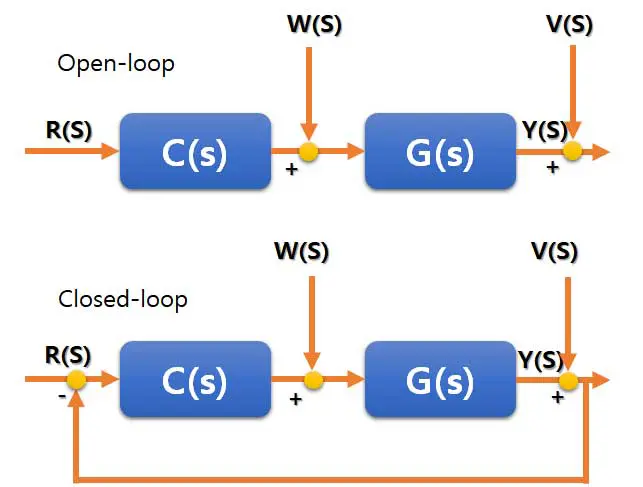
Open-loop

이 때 측정값 Y는 다음과 같다.

$Y=G(CR+W)$

외란이 존재할경우 GW 만큼의 오차가 항상 발생한다.

Closed-loop

이 경우는 다음과 같다.

$Y=G(C(R-Y-V)+W)$

$\rightarrow (1+CG)Y=CGR+GW-CGV$

$\rightarrow Y=\frac{CG}{1+CG}R+\frac{G}{1+CG}W-\frac{CG}{1+CG}V$

기준값을 추종하기 위해 R의 계수는 1로 만들어야하고

외란,잡음의 영향을 최소화 하기 위해 W,V의 계수는 0으로 만들어야 한다.

Open-loop 와 달리 피드백 제어는 C를 잘 설계하여 세가지를 다 만족시킬 수 있다.

loop shaping

R의 계수를 1로 만들고 W의 계수를 0으로 만드려면 C를 키워야한다.

하지만 V의 계수를 0으로 만드려면 C를 줄여야하기때문에 딜레마다.

다행히도 C(s)는 상수가 아니라 s에 대한 함수이기때문에

주파수 영역에 따라 다른 크기를 가지도록 설계할 수 있다.

Loop gain $L(s)$ 를 목적에 맞게 설계하는 것을 Loop shaping이라고 한다.

Open-loop gain에 대해 그래프로 나타내보자.

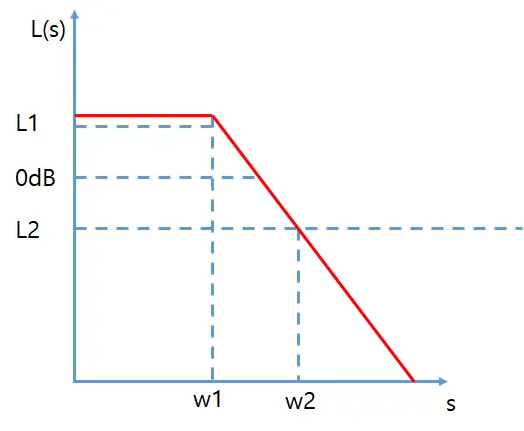
보통 R과 W는 저주파 영역에 졶재하고 V는 고주파 영역에 존재한다.

따라서 L(s)는 다음과 같은 조건을 가지면 목표성능을 만족시킬 수 있다.

저주파 영역 $(s<\omega_1): L(s)>L_1$
고주파 영역 $(s>\omega_2): L(s)<L_2$

이 조건대로 설계할 수 있는 방법론이 많지만 다음 제어기들이 가장 많이 쓰인다.

Lead, Lag 보상기
PID 제어기
H-infinity 제어기

추후에 이들 제어기에 대해서도 설명하겠다.